FoxCalculators - Calculadores gratuïtes en línia!

Un Eigenvector d'una matriu quadrada A és un vector no zero V que, quan la matriu es multiplica per V, produeix un múltiple constant de V, el multiplicador que es denota comunament per λ. Això és: a v = λ v

(Perquè aquesta equació utilitza la post-multiplicació per V, descriu un eigenvector correcte.) El nombre λ s'anomena valvalvale d'un corresponent a v.

Tots els valors propis i els vectors d'Eigenvectors satisfan l'equació AX = λx per a una matriu quadrada determinada A.

Calculadora de matriu simple per calcular el valor de l'EIGEN i el vector EIGEN d'una matriu 3x3. Introduïu els valors de la matriu 3x3 i feu clic al botó Calcular.

Dibuix

La traça, tr (a) d'una matriu quadrada A és la suma de les seves entrades diagonals. Mentre que la multiplicació de Matrix no és commutativa, com es va esmentar anteriorment, la traça del producte de dues matrius és independent de l'ordre dels factors:

TR (AB) = TR (BA).

Això és immediat des de la definició de la multiplicació de la matriu:

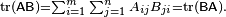
A més, la traça d'una matriu és igual a la de la seva transposició, és a dir,

tr (a) = tr (a ^{t ).}